트라이(Trie)
문자열에서의 검색을 빠르게 해주는 자료구조

장점
- M개의 문자로 구성된 문자열을 추가와 탐색하는 시간 복잡도는 O(M)
- 문자열을 빠르게 탐색할 수 있음
단점
- 필요한 메모리의 크기가 너무 큼
- 모두 소문자로만 이루어졌다고 해도, 26개의 공간이 필요

플로이드 와샬(Floyd-Warshall)
모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 알고리즘(방향, 음수 상관없음 / 싸이클이 발생하면 안됨)
- 단계마다 ‘거쳐 가는 노드’를 기준으로 알고리즘 수행
- 2차원 테이블에 최단 거리 정보를 저장
- DP 알고리즘에 해당
- 시간 복잡도는 O(N^3)
- 노드의 개수가 N개 일 때, N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 '현재 노드를 거쳐 가는 모든 경로'를 고려한다. 따라서 시간 복잡도는 총 O(N^3)임
- 점화식으로 설명할 수 있음

플로이드 워셜 알고리즘 그림으로 보기
[step 0] 그래프의 노드와 간선에 따라 최단 거리 테이블을 갱신한다.

[step 1] 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

[step 2] 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

[step ~] 3번, 4번, ... 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.


코드 구현
import sys
input = sys.stdin.readline
n = int(input())
m = int(input())
INF = float("inf")
arr = [[INF] * n for _ in range(n)]
for i in range(n):
arr[i][i] = 0
for i in range(m):
start, end, cost = map(int, input().split())
if arr[start - 1][end - 1] > cost:
arr[start - 1][end - 1] = cost
# 정점 탐색
for k in range(n):
# 모두 탐색
for i in range(n):
for j in range(n):
arr[i][j] = min(arr[i][j], arr[i][k] + arr[k][j])
for i in range(n):
for j in range(n):
if arr[i][j] == INF:
arr[i][j] = 0
print(arr[i][j], end=" ")
print()다익스트라(Dijkstra)
하나의 시작점으로부터 다른 모든 정점까지의 최단 거리를 구하는 알고리즘
- 여러 개의 노드가 있을 때, 특정한 노드에서 출발해 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘
- 음의 간선이 있을 경우 사용 불가
- 각 노드에 대한 현재까지의 최단 거리 정보’를 항상 1차원 리스트에 저장
- 시간 복잡도 O(V^2)
작동 방식
- 출발 노드를 설정
- 최단 거리 테이블을 초기화
- 방문하지 않는 노드 중에서 최단 거리가 가장 짧은 노드를 선택
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
- 3, 4번 과정 반복
동작 과정 그림으로 보기
[step 0] 그래프에서 시작 노드를 설정
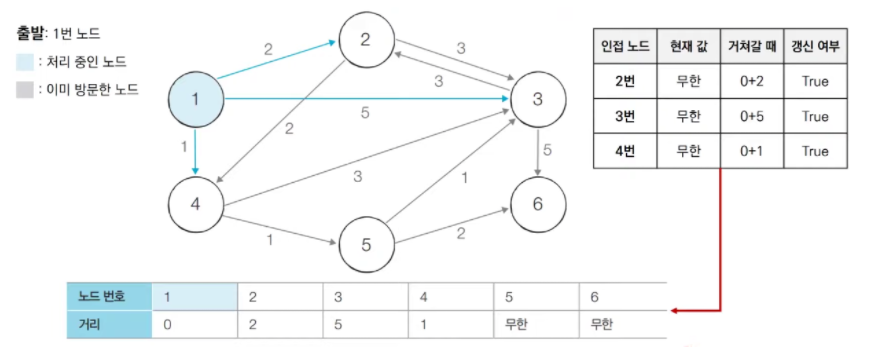
[step 1] 1번 노드를 시작으로 1번 노드와 연결되었고 방문하지 않은 노드를 처리

[step 2] 1번 노드와 연결된 노드 중 최단 거리가 가장 짧은 4번 노드를 방문하고, 4번 노드와 연결된 3번과 5번 노드의 거리 갱신
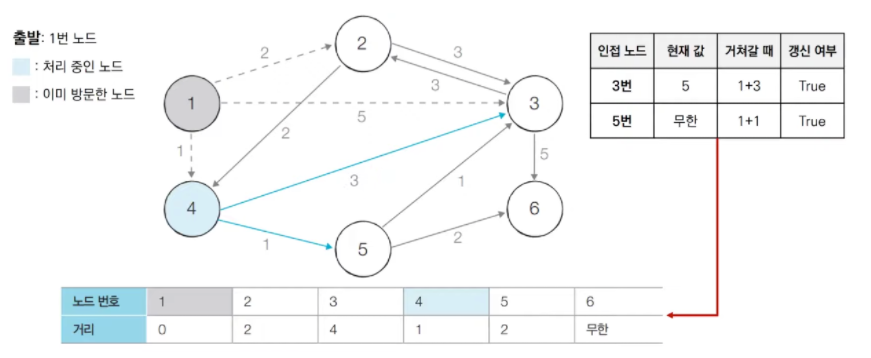
[step 3] 4번 노드가 처리됬으면 그 다음 최단 거리인 2번 노드를 처리한다. 이때 2번 노드와 연결된 3번 노드도 처리될텐데 1 -> 2 -> 3의 비용인 5보다 1 -> 4 -> 3의 비용이 작기 때문에 갱신되지 않는다. (최단 거리를 구하는 것이므로 무시된다.)

[step 4] 2번 노드가 처리됬으면 그 다음 최단 거리인 5번 노드를 처리한다. 5번 노드와 연결된 3번, 6번 노드의 거리 갱신

[step 5] 그 다음 최단 거리인 3번 노드를 처리

[step 6] 그 다음 최단 거리인 6번 노드를 처리

코드 구현
import heapq
graph = [
[0, 5, 0, 9, 2],
[5, 0, 2, 0, 0],
[0, 2, 0, 3, 0],
[9, 0, 3, 0, 2],
[2, 0, 0, 2, 0]
]
INF = float("inf") # 양의 무한대 설정
dist = [INF for _ in range(len(graph))]
dist[0] = 0
hq = []
def dijkstra(start):
heapq.heappush(hq, (dist[start], start))
while hq:
cur_cost, cur_node = heapq.heappop(hq)
if dist[cur_node] < cur_cost:
continue
for next_node, cost in enumerate(graph[cur_node]):
if cost != 0 and dist[next_node] > cur_cost + cost:
dist[next_node] = cur_cost + cost
heapq.heappush(hq, (dist[next_node], next_node))
dijkstra(0)
print(dist)우선순위 큐를 사용하는 다익스트라 알고리즘
- 우선순위의 기준 : 시작 노드와의 거리가 가장 가까운 노드(비용이 작은 것)
- 최단거리가 갱신될 경우에만 우선순위 큐에 넣음
- 시간 복잡도 : O(E log V) / E : 간선의 개수, V : 노드의 개수
다익스트라와 플로이드 와샬의 차이
- 다익스트라 알고리즘 : 하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구함
- 매번 가장 적은 비용을 가진 노드를 하나씩 꺼낸 다음 가장 적은 비용을 하나씩 선택하는 로직
- 플로이드 와샬 알고리즘 : 모든 정점에서 다른 모든 정점으로의 최단 경로를 구함
- 거쳐가는 정점을 하나씩 다 설정을 하여 거쳐가는 정점을 기준으로 최단 거리를 구하는 로직


[출처]
https://velog.io/@kimdukbae/%ED%94%8C%EB%A1%9C%EC%9D%B4%EB%93%9C-%EC%9B%8C%EC%85%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Floyd-Warshall-Algorithm
https://velog.io/@klloo/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4Trie-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0
'크래프톤 정글 - TIL' 카테고리의 다른 글
| 크래프톤 정글 5기 TIL - Day 16(알고리즘) (0) | 2024.04.03 |
|---|---|
| 크래프톤 정글 5기 TIL - Day 15(알고리즘) (1) | 2024.04.03 |
| 크래프톤 정글 5기 TIL - Day 13(알고리즘) (0) | 2024.04.01 |
| 크래프톤 정글 5기 TIL - Day 12(2)(프로세스) (0) | 2024.03.29 |
| 크래프톤 정글 5기 TIL - Day 12(CS:APP (1)) (0) | 2024.03.29 |
